Door joes op
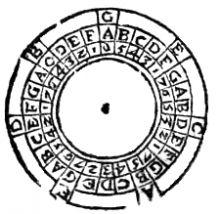
Nu we gezien hebben wat de concurrent is en wat de schrikkeldag, gaat het vervolg over de zonnecyclus, die als het ware voortkomt(1) uit deze jaren. Er is namelijk een zonnecyclus en dat is de tijdsduur waarin alle variaties voorvallen die in het zonnejaar door de concurrent en de schrikkeldag veroorzaakt kunnen worden. En deze cyclus is voltooid, wanneer er na het zevende jaar geen dagen overblijven na telling van de hele weken - waaruit de concurrenten voortkomen – en geen dagen gevormd uit de extra uren – waaruit het schrikkeljaar gevormd wordt. Deze tijdsduur is 28 jaar, aangezien al deze variaties in die tijd worden voltooid. En welk feest op welke dag gevierd wordt en op welke dag de schrikkeldag valt en dat zo een week wordt gevormd uit de schrikkeldagen in de hele cyclus, dat is te vinden in de onderstaande zonnecyclus met de tafel van de concurrenten:
En omdat de cyclus een cirkel is kunt u, waar u wilt het begin aanwijzen. Daarom is het niet te verwonderen, dat de zonnecyclus volgens verschillende geleerden op verschillende plaatsen begint. Hoe u de zonnecyclus op een gemakkelijke en correcte wijze indeelt, staat in het volgende vers:
Fons est dans bis agro, Fundus cibat, aufer edacem.
Augens fert escas, bos aut gens, edacibus glans.
De lettergrepen van deze verzen staan ieder voor één jaar in de volgorde van de zonnecyclus, dus de eerste voor het eerste jaar, de tweede voor het tweede enzovoort. Het nut van deze verzen is allereerst, dat u de zondagsletter weet. De letter waarmee de lettergreep begint, is namelijk de zondagsletter voor het hele jaar, tenzij het een schrikkeljaar betreft. In dat geval dient de zondagsletter voor tien maanden, te beginnen met Maart. En de letter die in de bovenste cirkel staat, is de zondagsletter voor Januari en Februari, tot aan de schrikkeldag. Ten tweede kunt u, zoals u weet, uit de zondagsletter onmiddellijk met het volgende vers de concurrent uitrekenen:
F.E.D.C.B.A.G. plaatsen de concurrenten.
Zo vaak namelijk F de zondagsletter is, is de concurrent 1, zo vaak E het is, 2, en zo voor de andere, als we volgorde van dit vers in acht nemen. Ten derde kunnen we eruit opmaken, welk jaar een schrikkeljaar is en welk niet. We moeten daarvoor zeven vingers van twee handen gebruiken. We beginnen voor het eerste jaar van de cyclus bij het onderste kootje van de wijsvinger van de linkerhand, het tweede is het middelste kootje, het derde het bovenste en het vierde de vingertop. Het vijfde is het onderste kootje van de middelvinger en zo gaan we door totdat de cyclus voltooid is. Dan zeg ik u, dat de zeven vingertoppen de schrikkeljaren aanduiden, de onderste kootjes het eerste jaar na een schrikkeljaar enzovoort. Dit is ook uit te rekenen uit de volgende omgekeerde alfabetische volgorde: G.F.E.D.C.B.A. Elke keer namelijk dat een letter in dit abc overspringt, hebben we te maken met een schrikkeljaar. En de letter die een extra sprong heeft gemaakt, is de zondagsletter gedurende tien maanden, zoals hierboven is gezegd. De letter van de eerste lettergreep die volgt, waar de sprong wordt gemaakt, zal gedurende tien maanden de zondagsletter zijn.(2) De ‘schrikkel’letters in de zeven schrikkeljaren, waaruit in de hele cyclus één week wordt gevormd, vinden we in het volgende vers:
Constans est genitor, bona donat, fertilis author.
Volgens Dionysius(3) echter, begint de zonnecyclus niet met dat jaar waar wij met Gerlandus(4) vanaf gaan tellen, maar met het twaalfde daarna, dat F als zondagsletter en 1 als concurrent heeft, zoals in het eerste jaar, maar het is een schrikkeljaar. De volgorde naar Dionysius wordt in het volgende vers beschreven:
Fallitur Eua dolo, cibus, Adae gaudia finit,
Et cum botrus adhuc germinet, Eua dolet.
Christus bella gerit, finitur eo duce bellum.
Ad grauidam fit dux, cuncta beauit Aue.
De truc om deze verzen te lezen is dezelfde als bij de vorige, alleen gaat het hier om woorden en niet om lettergrepen. En zij beginnen te tellen vanaf de top van de wijsvinger, dus vanaf een schrikkeljaar, en lopen over de toppen en de kootjes van de vingers, zoals hierboven. En de eerste letter van een woord is weer de zondagsletter. En we kunnen gewoon uitrekenen in het hoeveelste jaar van de cyclus we zijn, volgens zijn natuurlijke orde en het gebruik van de Kerk. Aan de jaren des Heren moeten twintig worden toegevoegd, want Christus is geboren in het eenentwintigste jaar. De hele som moet door 28 jaren worden gedeeld. Is dat gedaan en is de rest nul, dan zijn we in het laatste jaar van de cyclus. Is er een rest, dan toont dat getal aan in welk jaar van de cyclus wij ons bevinden. Maar indien u wilt weten in welk jaar van de Dionysische cyclus wij zitten, moeten aan de jaren des Heren 9 worden toegevoegd. Want het tiende jaar in de wenteling van de zonnecyclus, was het jaar voor Christus’ geboorte, zoals Abt Dionysius beweert. Deel de som door 28, als in de cyclus van Gerlandus, en u vindt wat u zoekt.
- ost geëmendeerd tot est.
- Het is mij niet duidelijk.
- Dionysius Exiguus (ca. 500- ca. 540) ontwierp de christelijke jaartelling en stelde de geboorte van Christus in het jaar 754 na de stichting van Rome. (Ik citeer uit de Katholieke Encyclopedie.)
- Gerlandus (ca. 1100) vond de methode uit om de concurrenten cyclisch te bepalen.
- Login om te reageren